hockey-stick identity

Topics

• pascal’s triangle

The Hockey Stick Identity is a combinatorial identity that states:

$$C(r,r)+C(r+1,r)+C(r+2,r)+\cdots +C(n,r)=C(n+1,r+1)$$

Here:

• $C(n,k)$ is the binomial coefficient
• The left-hand side (LHS) is the sum of binomial coefficients along a diagonal in Pascal’s Triangle.
• The right-hand side (RHS) is a single binomial coefficient.

Alternatively, it’s written as:

$$\begin{array}{r}\sum _{k=r}^n\left(\genfrac{}{}{0ex}{}{k}{r}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{r+1}\right)\\ \sum _{k=0}^{n-r}\left(\genfrac{}{}{0ex}{}{r+k}{r}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{r+1}\right)\\ \sum _{k=0}^{n-r}\left(\genfrac{}{}{0ex}{}{r+k}{k}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{r+1}\right)\end{array}$$

Replacing $n$ with $n+r$ in the last expression gives us the following equivalent identities, but whose “range” is from $r$ to $n+r$ (instead of $n$ previously):

$$\begin{array}{r}\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{r+k}{k}\right)=\left(\genfrac{}{}{0ex}{}{n+r+1}{r+1}\right)\\ \sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{r+k}{k}\right)=\left(\genfrac{}{}{0ex}{}{n+r+1}{n}\right)\end{array}$$

Relation to Pascal’s Triangle

In Pascal’s Triangle, the Hockey Stick Identity corresponds to summing elements along a diagonal. For example:

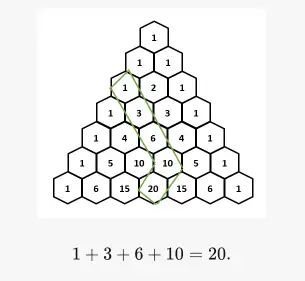
If we choose $r=2$, the sum of the diagonal $C(2,2)+C(3,2)+C(4,2)$ is:

$$C(2,2)+C(3,2)+C(4,2)=1+3+6=10$$

According to the Hockey Stick Identity, this sum equals $C(5,3)$:

$$C(5,3)=10$$

This matches the sum of the diagonal. The identity arises from the additive property of Pascal’s Triangle, where each entry is the sum of the two entries above it:

$$C(n,k)=C(n-1,k-1)+C(n-1,k)$$

When you sum along a diagonal, this additive property ensures that the sum telescopes to a single binomial coefficient. For example:

$$\begin{array}{rl}C(2,2)& =C(3,3)\\ C(3,2)& =C(4,3)-C(3,3)\\ C(4,2)& =C(5,3)-C(4,3)\end{array}$$

Adding these up cancels out intermediate terms, leaving only $C(5,3)$.

Note

There are several ways to prove the identity: proof 1, proof 2 (both leverage the double counting principle).

Related