water bottle

Topics

• geometry
• binary search

We have a box‐shaped (rectangular prism) bottle whose square base has side length $a$ and whose height is $b$. It is filled with $x$ cubic centimeters of water. We then tilt the bottle about one edge of its base and want to know the maximum tilt angle (from the upright position) before water starts to spill out.

Idea

This problem is a 3-D problem, but it is essentially a 2-D problem (since we are dealing with a rectangular prism with a square base). In other words, we can deal with “areas” instead of “volumes”. If $x$ is the volume of the water, then the cross-sectional area $S$ is $x/a$.

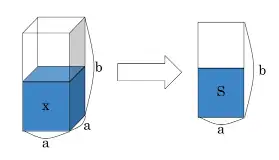
Approach 1 (Direct Solution)

Now, there are two main situations in which water can be spilled. The two cases come by comparing if the amount of water is more or less than “half” of the total area:

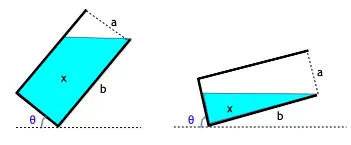
Mathematically, we can say:

• Case 1: $S>\frac{ab}{2}$
• Case 2: $S\le \frac{ab}{2}$

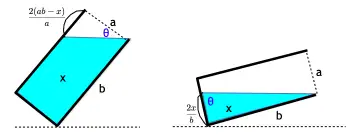
If you look at the geometry of Case 1:

• The area of the white right triangle is $ab-S$
• Basic trigonometry gives us the length of the other side to be $\frac{2(ab-S)}{a}$

Similarly, for Case 2:

• The area of a light blue right triangle is $S$
• Therefore, the length of the other side other comes to be $\frac{2S}{b}$

Now, it’s easy to calculate the angle $\theta$:

$$\begin{array}{rl}\text{Case 1:}& \tan \theta =\frac{\frac{2(ab-S)}{a}}{a}=\frac{2(ab-S)}{a^2}\\ \text{Case 2:}& \tan \theta =\frac{b}{\frac{2S}{b}}=\frac{b^2}{2S}\end{array}$$

Approach 2 (Binary Search)

Whether the water will be spilled or not when the bottle is tiled $\theta$ degrees is apparently monotonic, so the answer can be found by binary search boolean array framework. The condition will be to check if for a given angle $\theta$, $x$ is greater than the max volume of water than be filled in the bottle without spilling. If our check(degrees, ...) returns true for some degree, then for all angles larger than it, the result will also be true, since as we increase the inclination, we can store even lesser water.

In order to find out how much water can be stored/filled in the bottle at a given angle, without spilling, we need to tackle 2 potential cases. The diagrams below illustrate them. Note that since we have simplified our problem from 3-D to 2-D, we deal with areas instead of volumes.

Case 1

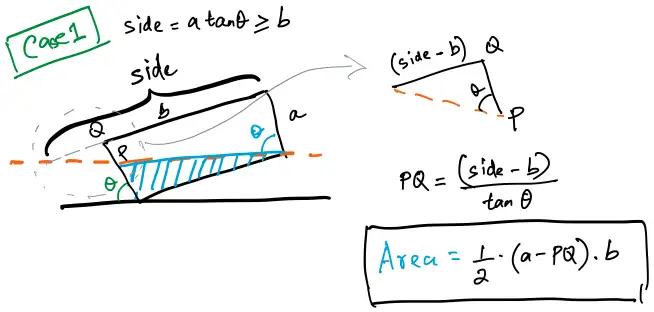
If you look at the geometry of Case 1:

• We can see that $\text{side}=a\tan \theta$
• In this case, $\text{side}\ge b$
• The length PQ can be calculated as $PQ=(\text{side}-b)/\tan \theta$
• The area of the empty triangle is $\text{Area}=\frac{1}{2}\cdot (a-PQ)\cdot b$

Case 2

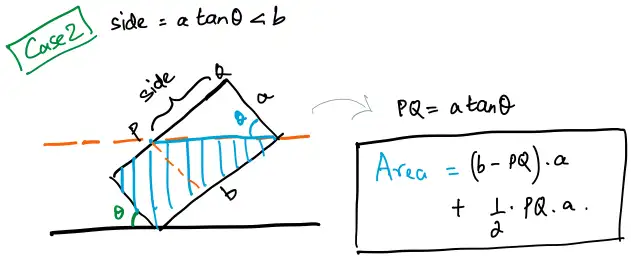
If you look at the geometry of Case 2:

• We can see that $\text{side}=a\cdot \tan \theta$
• In this case, $\text{side}<b$
• The length PQ is $PQ=\text{side}=a\cdot \tan \theta$
• The area of the water is the sum of a rectangle and a triangle: $\text{Area}=(b-PQ)\cdot a+\frac{1}{2}\cdot PQ\cdot a$

Note that since we are dealing with angles that can be floating point values, we apply binary search on real domain in our implementation. The time complexity is $O(50)\approx O(1)$ and the space complexity is $O(1)$.

Code

// Approach 1
void solve() {
  double a, b, x;
  cin >> a >> b >> x;
  double S = x / a; // S refers the cross-sectional "area"
  double rad;
  if (S >= (a * b) / 2) {
    // a*b - S = h*a/2
    // side = 2(a*b - S)/a
    double side = 2 * (a * b - S) / a;
    rad = atan2(side, a);
  } else {
    // S = side*b/2
    // side = 2S/b
    double side = 2 * S / b;
    rad = atan2(b, side);
  }
 
  const double PI = acos(-1.0);
  double deg = rad * 360 / (2 * PI); // radian to degrees
 
  cout << fixed << setprecision(10) << deg << '\n';
}
 
// Approach 2 (binary search)
bool check(double deg, double a, double b, double S) {
  double rad = deg * M_PI / 180;
  double area, side = a * tan(rad);
 
  if (side >= b) {
    // case 1
    double pq = (side - b) / tan(rad);
    area = (a - pq) * b / 2;
  } else {
    // case 2
    double pq = side;
    area = (b - pq) * a + (pq * a) / 2;
  }
 
  return area < S;
}
 
void solve() {
  double a, b, x;
  cin >> a >> b >> x;
  double S = x / a;
 
  double lo = 0;
  double hi = 90;
  double mid, ans = 0;
  double eps = 1e-6;
 
  for (int i = 0; i < 50; ++i) {
    mid = (lo + hi) / 2.0;
    if (check(mid, a, b, S)) {
      ans = mid;
      hi = mid - eps;
    } else {
      lo = mid + eps;
    }
  }
  cout << fixed << setprecision(10) << ans << endl;
}

Related