trapping rain water

Topics

• two pointers technique
• stacks
• greedy algorithm

Problem: Given an array of non-negative integers representing heights of bars, compute the amount of water that can be trapped between the bars if it rains.

Input: height = `[0,1,0,2,1,0,1,3,2,1,2,1]`
Output: 6

Idea

Approach 1

Water is trapped at a given index i if there are higher bars on both its left and right. The amount of water trapped at i is determined by the minimum of the maximum height seen so far from the left (max_left) and the maximum height seen so far from the right (max_right), minus the height of the bar at i itself.

The smaller side among height[left] and height[right] is limiting how much water can be trapped at that moment.

The amount of trapped water at an index i is:

$$\text{water}[i]=\max (0,\min (\text{max\_left},\text{max\_right})-\text{height}[i])$$

Important

Note that we are kind of calculating the contribution of trapped water from each bar. With this lens, we can say that this approach comes under contribution technique as welll

Algorithm (Two Pointers):

• Initialize:
  • Pointers: left = 0, right = n - 1
  • Max heights: max_left = 0, max_right = 0
• While left <= right:
  • Case 1: height[left] <= height[right]
    • Update max_left: max_left = max(max_left, height[left])
    • Add trapped water: trapped_water += max(0, max_left - height[left])
    • Move pointer: left += 1
  • Case 2: height[right] < height[left]
    • Update max_right: max_right = max(max_right, height[right])
    • Add trapped water: trapped_water += max(0, max_right - height[right])
    • Move pointer: right -= 1
• Return trapped_water

Time Complexity: $O(n)$ (single pass through the array).
Space Complexity: $O(1)$ (constant extra space for variables).

Approach 2

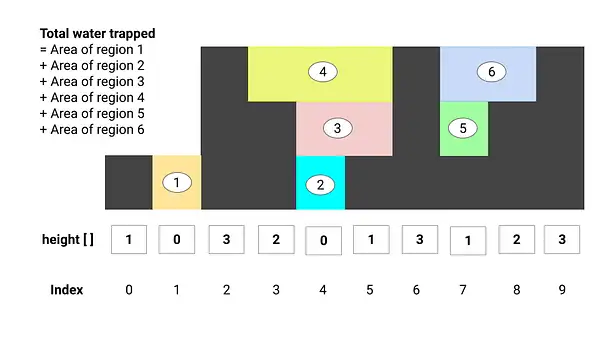
To solve the trapping rainwater problem using a stack, we leverage a monotonic stack approach. In the solution using 2 pointers (starting from the ends), we compute water vertically at each index and each bar’s contribution is summed up. In the stack based approach, we compute water in horizontal layers, by identifying segments where water is trapped between two boundaries.

Total water in the segment = width (distance) × depth (bounded height)

• Stack Usage: Maintain a stack storing indices of bars in decreasing order of their heights.
• Iterate through Bars: For each bar, check if it can act as a right boundary for previously encountered bars.
• Calculate Trapped Water: When a higher bar is found, pop the stack to compute water trapped between the popped bar, the new stack top (left boundary), and the current bar (right boundary).

Algorithm (Stack)

1. Initialize an empty stack
2. Iterate over each bar with index i:
   • While stack is not empty and height[i] > height[stack.top()]:
     • Pop the top element (top_idx). This is the bottom of the potential basin
     • If stack is empty, break (no left boundary)
     • Calculate distance = i - stack.top() - 1
     • Height = min(height[i], height[stack.top()]) - height[top_idx]
     • Add trapped water: distance * height
   • Push current index i onto the stack
3. Return total trapped water

Time Complexity: $O(n)$ (Each bar is pushed and popped exactly once)
Space Complexity: $O(n)$ (stack space)

Code

#############
# APPROACH 1 (2 pointers)
#############
def trap(height):
    n = len(height)
    if n == 0:
        return 0
 
    left, right = 0, n - 1
    max_left, max_right = 0, 0
    trapped_water = 0
 
    while left <= right:
        if height[left] <= height[right]:
            trapped_water += max(0, max_left - height[left])
            max_left = max(max_left, height[left])
            left += 1
        else:
            trapped_water += max(0, max_right - height[right])
            max_right = max(max_right, height[right])
            right -= 1
 
    return trapped_water
 
#############
# APPROACH 2 (stack)
#############
def trap(height):
    stack = []
    water = 0
 
    for i in range(len(height)):
        while stack and height[i] > height[stack[-1]]:
            top = stack.pop()
            if not stack:
                break
            distance = i - stack[-1] - 1
            bounded_height = min(height[i], height[stack[-1]]) - height[top]
            water += distance * bounded_height
        stack.append(i)
 
    return water

Related