search a 1D array reshaped as 2D matrix

Topics

• binary search
• matrices

Idea

Approach 1

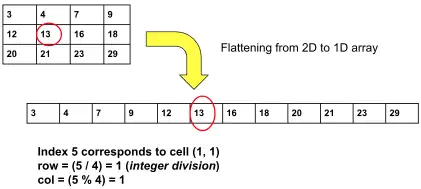
If we flatten the given 2D matrix to a 1D array (row major order), the 1D array will also be sorted. Turns out, we can apply binary search on the 1D array without actually flattening the 2D matrix, by figuring out the indices correctly (using basic modular arithmetic)

T.C: $O(\log (n\times m))$
S.C: $O(1)$

Approach 2

Another way to implement this is to simply find the correct row using binary search and then in that row, find the value using binary search again.

T.C: $O(\log n+\log m))=O(\log (n\times m))$
S.C: $O(1)$.

Approach 3

Start at either the top-right or the bottom left corner of the matrix and efficiently eliminate either a row or a column in each comparison. Basically, reach at the correct row (or column) and then do a linear scan on that row or col.

Let’s say, we start at bottom-left corner: If the current element is greater than the target, we can eliminate the rows below it (including current row), i.e. i -= 1. If the current element is smaller than the target, we can be sure that the target (if exists) has to be in the current row, so we move across the columns to the right, i.e. j += 1.

T.C: $O(m+n)$
S.C: $O(1)$

Code

###############
# Approach 1
###############
def searchMatrix(matrix, target):
    n = len(matrix)
    m = len(matrix[0])
 
    # apply binary search:
    low = 0
    high = n * m - 1
    while low <= high:
        mid = (low + high) // 2
        row = mid // m
        col = mid % m
        if matrix[row][col] == target:
            return True
        elif matrix[row][col] < target:
            low = mid + 1
        else:
            high = mid - 1
    return False
 
###############
# Approach 2
##############
def searchMatrix(self, matrix, target):
    if not matrix or not matrix[0]:
        return False
 
    rows = len(matrix)
    cols = len(matrix[0])
 
    # Find the correct row
    row_index = -1
    low = 0
    high = rows - 1
    while low <= high:
        mid = (low + high) // 2
        if matrix[mid][0] <= target:
            row_index = mid  # Potential row, but keep searching rows below
            low = mid + 1
        else:
            high = mid - 1
 
    if row_index == -1:  # Target is smaller than all first elements
        return False
 
    # Find target in the row
    low = 0
    high = cols - 1
    while low <= high:
        mid = (low + high) // 2
        if matrix[row_index][mid] == target:
            return True
        elif matrix[row_index][mid] < target:
            low = mid + 1
        else:
            high = mid - 1
 
    return False
 
 
###############
# Approach 3
##############
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
    n, m = len(matrix), len(matrix[0])
    i, j = n-1, 0
    while (0 <= i < n) and (0 <= j < m):
        curr = matrix[i][j]
        if (curr == target): return True
        elif (curr < target): j += 1
        else: i -= 1
 
    return False

Related