number of parts in convex polygon

Topics

• geometry
• combinatorics
• contribution technique

You have given Convex N-gon. Draw all diagonals of the convex N-gon. Suppose no three diagonals pass through a point. Into how many parts is the N-gon divided?

Input:
2 (num test cases)
4
5
Output:
4
11

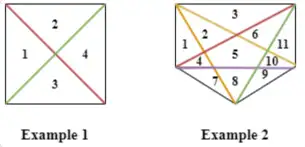
Idea

1. Start with one region
   A convex n-gon is one whole region before any diagonals are drawn
2. Count the diagonals
   There are $\frac{n(n-3)}{2}$ diagonals in an n-gon. If you imagine drawing a diagonal that doesn’t intersect any others, it would simply cut one region into two, thus “contributing” one new region. So, if the diagonals didn’t cross, you would contribute $\frac{n(n-3)}{2}$ regions
3. Count the intersections
   Any set of 4 vertices forms a convex quadrilateral, and its two diagonals cross exactly once. Thus, the total number of intersection points is $\left(\genfrac{}{}{0ex}{}{n}{4}\right)$
4. Each intersection adds one region
   When a new diagonal is drawn, if it crosses already-drawn diagonals, each crossing splits an existing segment of the diagonal, thereby increasing the total count of regions. Summing over the process, each intersection contributes an extra region
5. Putting it all together:
   • Start with 1 region.
   • Add $\frac{n(n-3)}{2}$ regions (one per diagonal).
   • Add $\left(\genfrac{}{}{0ex}{}{n}{4}\right)$ regions (one per intersection).

Thus, the total number of regions inside the n-gon is

$$\boxed{R(n)=1+\frac{n(n-3)}{2}+\left(\genfrac{}{}{0ex}{}{n}{4}\right)}$$

This elegant formula arises from counting the “cuts” made by the diagonals and their intersections in a systematic way.

Code

ll MOD = 1000000007;
 
ll binpow(ll a, ll b) {
  if (b == 1)
    return a % MOD;
 
  ll tres = binpow(a, b >> 1);
  ll res = (tres * tres) % MOD;
  if (b & 1)
    res = (res * a) % MOD;
  return res;
}
 
ll inv(ll a) { return binpow(a, MOD - 2); }
 
ll nCr(ll n, ll r) {
  ll res = 1;
  for (int i = 0; i < r; ++i) {
    res = (res * (n - i)) % MOD;
    res = (res * inv(i + 1)) % MOD;
  }
  return res;
}
 
void solve() {
  ll n;
  cin >> n;
 
  // straightforward formula application
  ll res = 1 + ((n*(n-3) % MOD) * inv(2))%MOD + nCr(n, 4);
  cout << (res + MOD) % MOD << endl;
}

Implementation relies on efficient binomial coefficient using factorials calculation.

Related