Embedding vs Linear layer in PyTorch

Topics

• pytorch-internals
• word embeddings

Embedding layers are at the heart of almost every NLP architecture since the past decade. We are all familiar with nn.Linear layers. Turns out, nn.Embedding is simply a lookup table.

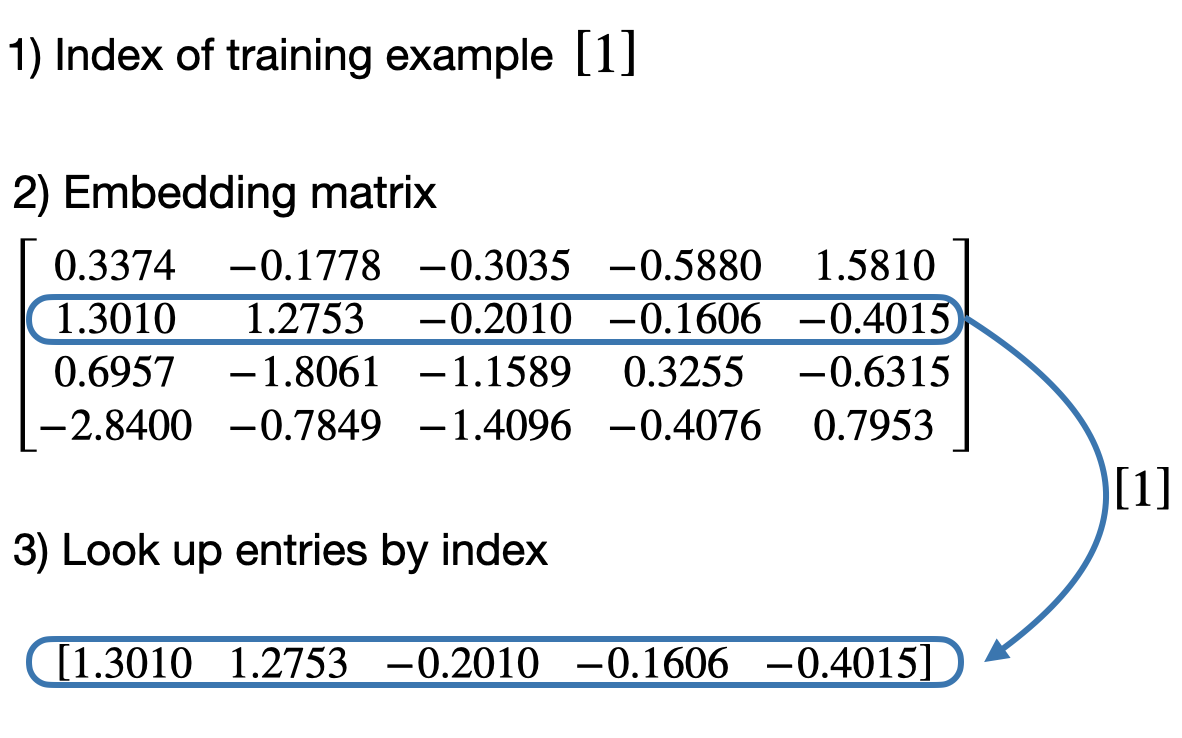
The embeding layer above accomplishes exactly the same as nn.Linear layer (without bias term) on a one-hot encoded representation in PyTorch.

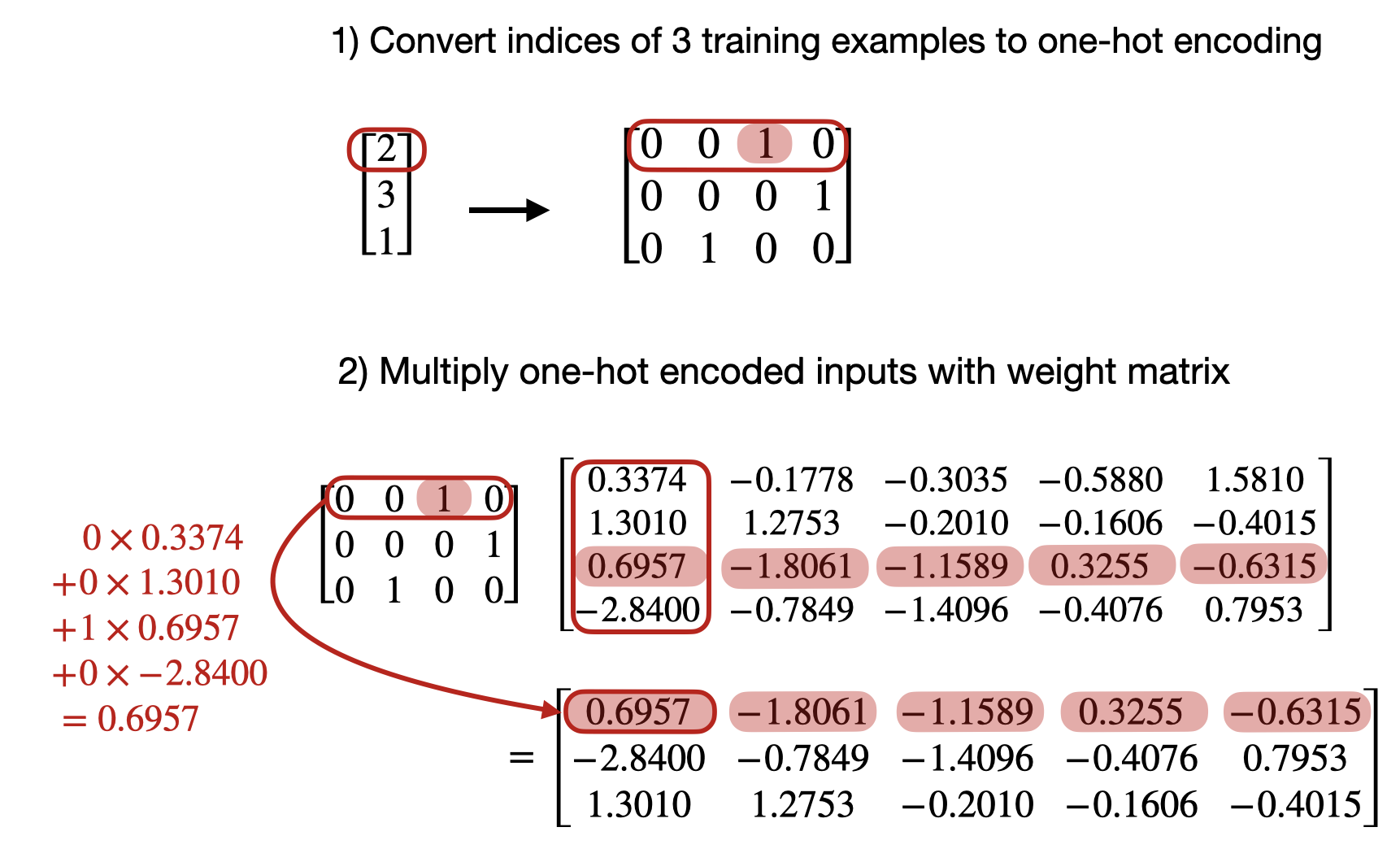
Since all but one index in each one-hot encoded row are 0 (by design), this matrix multiplication is essentially the same as a look-up of the one-hot elements.

V=4
dims=5
 
embedding = torch.nn.Embedding(V, dims) 
linear = torch.nn.Linear(V, dims, bias=False)
 
print(embedding.weight.shape) # torch.Size([4, 5])
print(linear.weight.shape) # torch.Size([5, 4])

To make an apples to apples comparison, let’s have the weights equal in them

linear.weight = torch.nn.Parameter(embedding.weight.T)

For linear layer, we need input to be one-hot encoded

idx = torch.tensor([2, 3, 1])
onehot_idx = torch.nn.functional.one_hot(idx)

Comparing the results:

res_linear = linear(onehot_idx.float())
res_emb = embedding(idx)
 
torch.allclose(res_linear, res_emb) # True

Thus, we see nn.Embedding and nn.Linear (without bias term) work the same.

Even though nn.Embedding and nn.Linear essentially work the same, there are few reasons to prefer nn.Embedding for lookups:

• Efficient implementation
• For nn.Linear, lot of wasteful multiplications by 0
• Memory acess pattern: For nn.Linear, entire weight matrix is loaded in memory during forward pass
• During backpopagation, entire weight matrix is updated (most updates are 0 though)