Topics
A kernel function (in the context of ML) computes the inner product between vectors in a different feature space. , where is the mapping to the feature space. Popular kernel functions include:
- Linear Kernel is the simplest: . This is just a standard dot product in the original input space. It’s efficient for large datasets, especially text data, and effective when data is linearly separable
- Polynomial Kernel maps data to a polynomial feature space: . It captures polynomial interactions between features. Parameters are degree (), scale (), and offset (). A degree of 1 with is equivalent to the linear kernel. Higher degrees can capture more complex boundaries but increase the risk of overfitting
- Radial Basis Function (RBF) Kernel, also known as the gaussian kernel, uses the distance between points: . This kernel corresponds to an infinite-dimensional feature space and can capture complex, non-linear regions. It’s often a good default choice when prior knowledge about the data is limited. The parameter scales the distance
- Sigmoid Kernel is defined as: . It resembles the activation function used in neural networks
Some other kernels include ANOVA radial basis, hyperbolic tangent, and Laplace RBF.
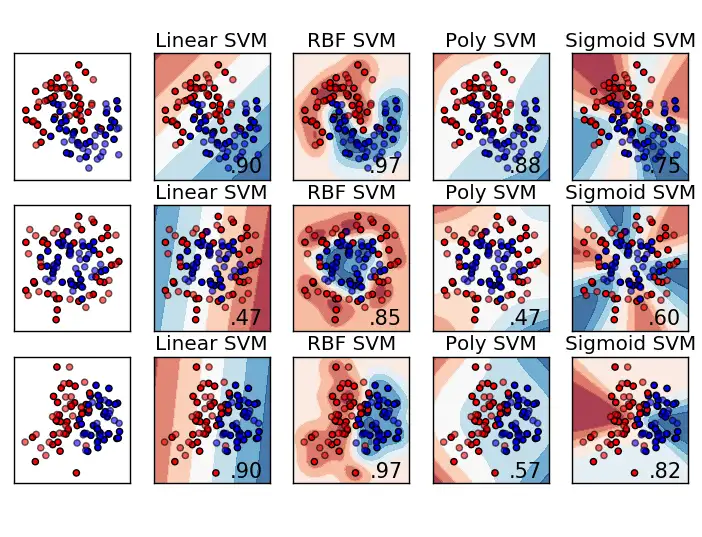
Choosing the best kernel depends on the specific problem and data characteristics. The linear kernel is fast for linearly separable data. RBF is versatile when data distribution is unknown. Polynomial kernels work well when data is normalized. No matter which kernel we choose, you will need to tune the kernel parameters to get good performance from the classifier. Popular parameter-tuning techniques include k-fold cross validation.