Topics
As the dimensionality increases, the number of data points required for good performance of any machine learning algorithm increases exponentially. The reason is that, we would need more number of data points for any given combination of features, for an ML model to be valid.
Data Sparsity
Sparsity of data occurs when moving to higher dimensions. The volume of the space represented grows so quickly that the data cannot keep up and thus becomes sparse
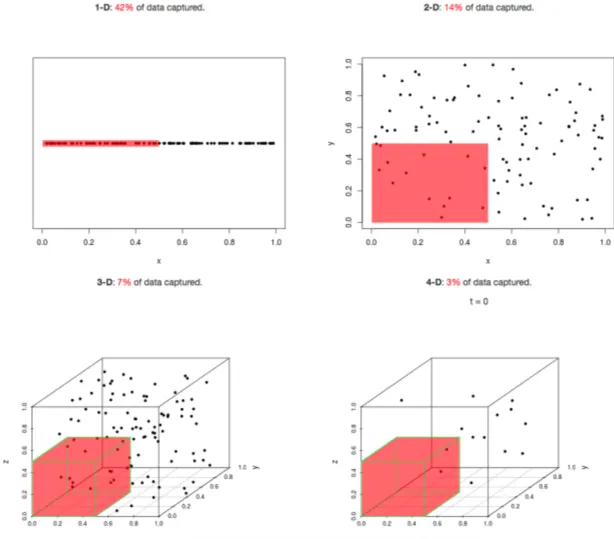
As the data space seen above moves from one dimension to two dimensions and finally to three dimensions, the given data fills less and less of the data space (becomes sparse). In order to maintain an accurate representation of the space, the amount of needed data for analysis grows exponentially.
Example
Let’s say that for a model to perform well, we need at least 10 data points for each combination of feature values. If we assume that we have one binary feature, then
- For its unique values (0 and 1) we would need data points.
- For -number of binary features we would need data points.
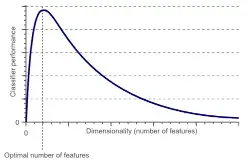
Hughes (1968) in his study concluded that with a fixed number of training samples, the predictive power of any classifier first increases as the number of dimensions increase, but after a certain value of number of dimensions, the performance deteriorates. Thus, the phenomenon of curse of dimensionality is also known as Hughes phenomenon.