hinge loss

Topics

• loss functions

Hinge loss measures a penalty based on a data point’s position relative to the classification margin. It’s centrally used in soft margin objective in SVM. The objective there is to minimize a combination of the weight vector norm (to maximize margin) and the total hinge loss (to penalize “margin violations”).

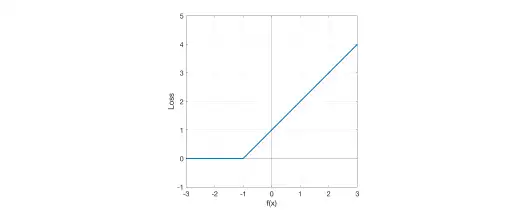
Formula: For a true label $y\in \{-1,+1\}$ and model output score $f(x)=w^{T}x+b$:

$$L_{\text{hinge}}(y,f(x))=\max (0,1-yf(x))$$

• If $yf(x)\ge 1$: Point is correctly classified (for SVM, on or outside the correct margin boundary). Loss = 0. No penalty
• If $yf(x)<1$: Point violates the margin (for SVM, either inside margin but correct side, or misclassified). Loss = $1-yf(x)$. Penalty increases linearly

Note

Connection to Slack Variables: In soft margin SVM, slack variable ${\xi }_i$​ represents the hinge loss for point $i$: ${\xi }_i\ge \max (0,1-y_i(w^T{x}_i+b))$. Minimizing $C\sum {\xi }_i$​ in the soft margin objective in SVM is equivalent to minimizing total hinge loss (plus regularization term).

Hinge loss is convex and hence suitable for optimization. However, hinge loss is not differentiable at $yf(x)=1$. Despite this, it has a subgradient, allowing algorithms like gradient descent to be used. Smoothed versions of hinge loss can also be used for optimization.

import numpy as np
def hinge_loss(y_true, score): # y_true is -1 or 1
  return np.maximum(0, 1 - y_true * score)

Usefulness:

• Hinge loss tends to lead to sparse models, meaning many training samples do not influence the final model (e.g. only the support vectors do in case of SVM)
• It’s less sensitive to outliers than squared loss (penalty increases linearly, not quadratically)
• Compared to logistic regression, which uses binary cross entropy loss (Log loss), the Hinge Loss aims more directly at maximizing the margin rather than estimating probabilities

Related