derangement recurrence

Topics

• derangements
• recursion

We need to count the number of ways to permute n elements such that no element appears in its original position.

Using recurrence, we can get:

$$D(n)=(n-1)\times (D(n-1)+D(n-2))$$

where $D(0)=1$ (there’s one way to arrange nothing - an empty permutation) and $D(1)=0$ (you can’t arrange one element so it’s not in its original spot).

Intuition Behind the Formula:

Let’s say we have n items. Consider the first item. It can go into any of the (n-1) other positions. Let’s say it goes into position i. Now, there are two possibilities:

1. The i-th item goes into the first position. Then, we have (n-2) remaining items, and we need to derange them, which can be done in D(n-2) ways
   
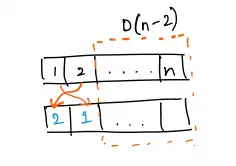
2. The i-th item doesn’t go into the first position. Now, we can think of the first position as the “forbidden” position for the i-th item. So, we have (n-1) items, and we need to derange them, which can be done in D(n-1) ways
   

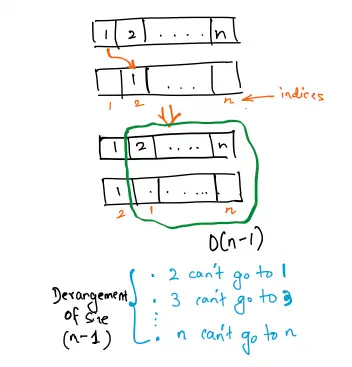
Therefore, D(n) = (n-1) * [D(n-1) + D(n-2)].

long long derangement(int n) {
    if (n == 0) return 1;
    if (n == 1) return 0;
    return (n - 1) * (derangement(n - 1) + derangement(n - 2));
}

Note that this recursive implementaion is very similar to the fibonacci series implementation. Additionally, we can convert a recursive solution to an iterative one. In this case, the iterative version would be:

const int MOD = 1e9+7;
 
int derangement(int n) {
    if (n == 0) return 1;
    if (n == 1) return 0;
 
    long long a = 1, b = 0, c;
    for (int i = 2; i <= n; i++) {
        c = (i - 1) * (a + b) % MOD;
        a = b;
        b = c;
    }
    return c;
}

Note

There’s another derangement recurrence dervied from direct formula. That is easier to implement in competitive programming

Related

• derangement direct formula