catalan number direct formula combinatorial proof

Topics

• catalan number

Catalan numbers are a fascinating sequence of numbers appearing in various counting problems in combinatorics. One of the most intuitive ways to understand and derive the formula for Catalan numbers is through the lens of grid paths.

Imagine an $n\times n$ grid, starting from coordinate $(0,0)$ at the bottom-left and ending at $(n,n)$ at the top-right. We are interested in paths from $(0,0)$ to $(n,n)$ that only move right (R) or up (U), often called monotonic paths. Each such path consists of exactly $n$ right steps and $n$ up steps, making a total of $2n$ steps.

1. Counting All Paths

First, let’s determine the total number of monotonic paths from $(0,0)$ to $(n,n)$ without any restrictions. We have $2n$ steps in total, and we need to choose $n$ of them to be right steps (or equivalently, $n$ to be up steps). The number of ways to do this is given by the binomial coefficient:

$$\text{Total Paths}=\left(\genfrac{}{}{0ex}{}{2n}{n}\right)=\frac{(2n)!}{n!n!}$$

2. Defining “Good” and “Bad” Paths

Now, let’s introduce a condition. We are interested in paths that do not go above the main diagonal, the line connecting $(0,0)$ to $(n,n)$, which is given by the equation $y=x$. A “good” path is a monotonic path from $(0,0)$ to $(n,n)$ that stays on or below the main diagonal. A “bad” path, on the other hand, is a monotonic path from $(0,0)$ to $(n,n)$ that crosses above the main diagonal, meaning it goes above the line $y=x$ at some point. Our goal is to count the number of “good” paths, which is given by the Catalan numbers.

3. The Reflection Principle: Mapping Bad Paths

To count “good” paths, we will use a clever trick to count “bad” paths instead, and then subtract this count from the total number of paths. The reflection principle provides a beautiful way to count “bad” paths.

Consider a “bad” path. Since it starts at $(0,0)$ (where $y=x$) and ends at $(n,n)$ (where $y=x$), and it crosses above the main diagonal, it must at some point touch the line $y=x+1$, which is the diagonal just above the main diagonal. Let’s find the first point where a “bad” path touches the line $y=x+1$. Let’s call this point $P$.

Now, for the portion of the path after this point $P$, we perform a reflection across the line $y=x+1$. What does this reflection do? Whenever the original path takes a right step (R), the reflected path takes an up step (U), and whenever the original path takes an up step (U), the reflected path takes a right step (R). In essence, for every step after point $P$, we swap right steps with up steps and vice versa.

4. Understanding the Reflected Path’s Endpoint

Let’s analyze where this reflection takes us. Suppose the point $P$ is $(a,a+1)$ (since it lies on $y=x+1$). Consider the portion of the “bad” path from $(0,0)$ to $(n,n)$. Let’s break it into two parts: the part before $P$ and the part from $P$ to $(n,n)$. The part before $P$ remains unchanged. We only reflect the part after $P$.

Let’s think about the number of steps in the reflected portion. Suppose from $P$ to $(n,n)$, the original “bad” path had $r$ right steps and $u$ up steps. Then, in the reflected path, this portion will have $u$ right steps and $r$ up steps. The total number of steps in the portion from $P$ to $(n,n)$ is still $r+u$.

Crucially, when we reflect the path after the first touch at $y=x+1$, consider the number of right and up steps. In the original “bad” path from $(0,0)$ to $(n,n)$, there are $n$ right steps and $n$ up steps in total. Let’s analyze the section of the path before the first touch of $y=x+1$ at point $P=(a,a+1)$. To reach $(a,a+1)$ from $(0,0)$ staying below or on $y=x+1$, we must have taken some number of right steps and up steps. At point $P=(a,a+1)$, the x-coordinate is $a$ and y-coordinate is $a+1$. So to reach $P$, we have taken $a$ right steps and $a+1$ up steps in the part of the path before $P$.

For a “bad” path, before reflection up to point $P=(a,a+1)$:

• Number of right steps = $a$
• Number of up steps = $a+1$
• Total steps to $P=2a+1$.

Remaining steps from $P$ to $(n,n)$ in the original “bad” path:

• Number of remaining right steps = $n-a$
• Number of remaining up steps = $n-(a+1)=n-a-1$
• Number of reflected right steps = $n-a-1$
• Number of reflected up steps = $n-a$

So the endpoint of the reflected path will be:
x-coordinate: (x-coordinate of $P$) + (Number of reflected right steps) = $a+(n-a-1)=n-1$
y-coordinate: (y-coordinate of $P$) + (Number of reflected up steps) = $(a+1)+(n-a)=n+1$

Therefore, every “bad” path from $(0,0)$ to $(n,n)$ is transformed into a path from $(0,0)$ to $(n-1,n+1)$.

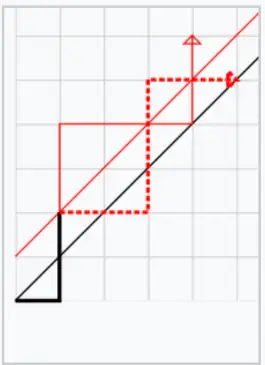
Black diagonal: $y=x$. red diagonal: $y=x+1$. The invalid portion of the path (dotted red) is flipped (solid red). Bad paths (after the flip) reach $(n-1,n+1)$ instead of $(n,n)$.

5. Bijection and Reversibility

The reflection establishes a bijection because every monotonic path from $(0,0)$ to $(n-1,n+1)$ is guaranteed to touch the higher diagonal $y=x+1$. This is because such paths start with $y-x=0$ and end with $y-x=2$, requiring a passage through $y-x=1$. Also, the reflection process itself is reversible; applying it twice brings us the original path. Therefore, this reflection creates a one-to-one correspondence between the set of “bad” paths in the $n\times n$ grid and the set of all monotonic paths in the $(n-1)\times (n+1)$ grid.

6. Counting Bad Paths and Catalan Numbers

The number of monotonic paths from $(0,0)$ to $(n-1,n+1)$ is:

$$\text{Number of Bad Paths}=\left(\genfrac{}{}{0ex}{}{(n-1)+(n+1)}{n-1}\right)=\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right)=\left(\genfrac{}{}{0ex}{}{2n}{n+1}\right)$$

Recall that the total number of monotonic paths from $(0,0)$ to $(n,n)$ is $\left(\genfrac{}{}{0ex}{}{2n}{n}\right)$. The number of “good” paths (Catalan numbers, $C_n$) is the total number of paths minus the number of “bad” paths:

$$C_n=\text{Total Paths}-\text{Bad Paths}=\left(\genfrac{}{}{0ex}{}{2n}{n}\right)-\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right)$$

We can simplify this expression:

$$C_n=\left(\genfrac{}{}{0ex}{}{2n}{n}\right)-\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right)=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}$$ $$\begin{array}{rl}{C}_n& =\frac{(2n)!}{n!(n-1)!}\left[\frac{1}{n}-\frac{1}{n+1}\right]\\ & =\frac{(2n)!}{n!(n-1)!}\left[\frac{(n+1)-n}{n(n+1)}\right]\\ & =\frac{(2n)!}{n!n!}\frac{1}{(n+1)}\end{array}$$

Thus, the $n$-th Catalan number is given by the formula:

$$\boxed{C_n=\frac{1}{n+1}\left(\genfrac{}{}{0ex}{}{2n}{n}\right)}$$

Related

• catalan number recurrence proof