c3 linearization

Topics

• python internals
• oops

In object-oriented systems with multiple inheritance, some mechanism must be used for resolving conflicts when inheriting different definitions of the same property from multiple superclasses. C3 superclass linearization is an algorithm used primarily to obtain the order in which methods should be inherited in the presence of multiple inheritence. In other words, the output of C3 superclass linearization is a deterministic Method Resolution Order (MRO).

C3 superclass linearization is called C3 because it “is consistent with three properties:

• a consistent extended precedence graph
• preservation of local precedence order, and
• fitting a monotonicity criterion

Algorithm

Core Principle: Linearization L[C] of a class C is calculated as: L[C] = [C] + merge(L[P1], L[P2], ..., L[Pn], [P1, P2, ..., Pn]) where P1, P2, ..., Pn are direct parent classes of C, in order.

Merge Algorithm (merge(L1, L2, ..., Ln)): Takes a list of sequences (linearizations of parents and list of parents). Repeatedly finds the next class to add to the result:

Notation: L1 is a sequence say: [A, B, C], A is the head and [B, C] is the tail.

1. Look at heads of first non-empty sequences
2. Select head H of the first non-empty sequence Li if H does not appear in the tail of any other non-empty sequence Lj (where j != i)
3. If a head H is selected:
   • Add H to result list
   • Remove H from all sequences where it appears as the head
   • Go back to step 1
4. If no head can be selected from any non-empty sequence, merge fails (often indicates inconsistent inheritance structure)
5. If all sequences are empty, merge successful

class O
class A extends O
class B extends O
class C extends O
class D extends O
class E extends O
class K1 extends C, A, B
class K3 extends A, D
class K2 extends B, D, E
class Z extends K1, K3, K2

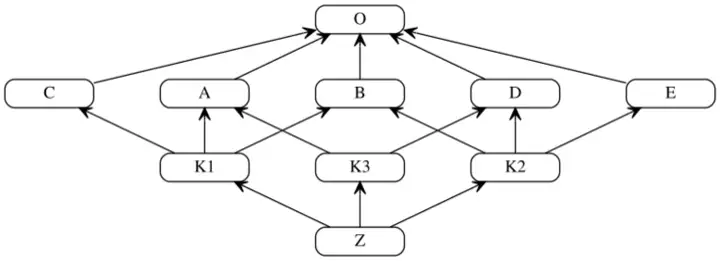
Worked Example

Given class hierarchy:

• Base class: O (object)
• Intermediate: A,B,C,D,E all inherit from O
• Layer 1:
  • K1 inherits from C,A,B
  • K3 inherits from A,D
  • K2 inherits from B,D,E
• Top: Z inherits from K1,K3,K2

Linearizations:

1. Base cases (all inherit directly from O):

   • L(O) = [O]
   • L(A) = [A, O]
   • Similarly for B,C,D,E

2. First complexity level (K1,K3,K2):

   • L(K1) = [K1] + merge([C,O], [A,O], [B,O], [C,A,B]):
     Steps: select C → A → B → O
     Result: [K1, C, A, B, O]
   • L(K3) = [K3] + merge([A,O], [D,O], [A,D]):
     Steps: A → D → O
     Result: [K3, A, D, O]
   • L(K2) = [K2] + merge([B,O], [D,O], [E,O], [B,D,E]):
     Steps: B → D → E → O
     Result: [K2, B, D, E, O]

3. Final case (Z):

   • L(Z) = [Z] + merge([K1,C,A,B,O], [K3,A,D,O], [K2,B,D,E,O], [K1,K3,K2])
     Steps: K1 → C → K3 → A → K2 → B → D → E → O
     Final order: [Z, K1, C, K3, A, K2, B, D, E, O]

In Python we find the MRO as follows:

# ... rest of the classes
class Z(K1, K3, K2): pass
 
print(Z.mro())
 
# Output: [Z, K1, C, K3, A, K2, B, D, E, O, <class 'object'>]

Related

• diamond inheritance problem