Altamash Khan

Altamash Khan

Did the war forge the spear that remained? No. All it did was identify the spear that wouldn't break

Altamash Khan

Altamash Khan

Did the war forge the spear that remained? No. All it did was identify the spear that wouldn't break

𖤍

2D prefix sums

Mar 20, 20252 min read

Topics

The concept of partial sums extends naturally to two-dimensional arrays (matrices). A 2D partial sum matrix PS for a matrix M is defined such that PS[i][j] stores the sum of all elements in the sub-rectangle from M[0][0] to M[i][j]. Constructing the prefix matrix as well as doing range sum query leverages (inclusion-exclusion principle):

We want the sum of the rectangle up to (i, j). We can achieve this by:

  1. Taking the sum of the rectangle up to (i-1, j): PS[i-1][j]
  2. Taking the sum of the rectangle up to (i, j-1): PS[i][j-1]
  3. Notice that the rectangle up to (i-1, j-1) has been added twice (once in step 1 and once in step 2). We need to subtract it once: - PS[i-1][j-1]
  4. Finally, add the current element M[i][j]

Thus, formula is: PS[i][j] = PS[i-1][j] + PS[i][j-1] - PS[i-1][j-1]

Once prefix sum array is constructed, we are usually asked to answer range queries (for sums). We have the formula as:

SumRectangle(r1, c1, r2, c2) = PS[r2][c2] - PS[r1-1][c2] - PS[r2][c1-1] + PS[r1-1][c1-1]

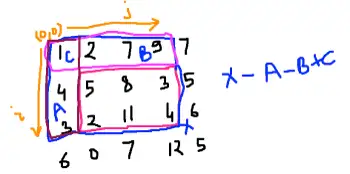
Explanation:

  1. PS[r2][c2] includes the sum of the entire rectangle from (0, 0) to (r2, c2).
  2. PS[r1-1][c2] (if r1 > 0) removes the sum of the rectangle above our target rectangle (from (0, 0) to (r1-1, c2)).
  3. PS[r2][c1-1] (if c1 > 0) removes the sum of the rectangle to the left of our target rectangle (from (0, 0) to (r2, c1-1)).
  4. PS[r1-1][c1-1] (if r1 > 0 and c1 > 0) was subtracted twice (once in step 2 and once in step 3), so we need to add it back to correct for the over-subtraction. This rectangle represents the area that was removed twice.

Backlinks